Inteligjenca Artificiale: Struktura e Rrjeteve Nervore

Rrjeti nervor artificial është koncepti dhe mjeti më i rëndësishëm i inteligjencës artificiale për shkak të rolit të tij thelbësor në zbatimet e suksesshme të kësaj fushe studimore në drejtime nga më të ndryshmet. Fuqia e madhe e tij buron nga aftësia e trajnimit me të dhëna duke mësuar përfaqësime sa më të përshtatshme të tyre çka bën të mundur lidhjen e të dhënave me parashikimet që na nevojiten. Nga kjo pikëpamje, rrjetet nervore mësojnë se si të lidhin të dhënat dhe vlerat e madhësive që parashikohen prej tyre. Aftësia parashikuese e rrjeteve nervore rrjedh nga struktura hierarkike apo shumështresore e tyre. Rrjeti i parë nervor i quajtur Perceptron u shpik në vitin 1958 nga Rozenblat (Frank Rosenblatt, 1928–1971). Perceptroni ishte në fakt një rrjet shumë i thjeshtë i përbërë nga vetëm një nyjë (neuron) e cila mblidhte sinjalet e peshuar të hyrjes dhe aktivizohej për të dhënë vlerën e parashikuar në dalje (për më shumë rreth Perceptronit kalo këtu). Rrjetet nervore që u projektuan më vonë u bazuan te rrjeti Perceptron duke e zgjeruar atë në mënyra të ndryshme.
Në figurën më sipër paraqitet skema e përgjithshme e një rrjeti nervor shumështresor. Njësia apo nyja bazë e çdo rrjeti nervor është neuroni, një njësi përllogaritëse e thjeshtë që merr në hyrje sinjale të peshuara dhe gjeneron në dalje një sinjal që varet nga shuma e hyrjeve dhe nga funksioni i aktivizimit që neuroni përdor. Përveç sinjaleve të hyrjes, secili neuron pranon shpesh si hyrje edhe një vlerë animi (ang. bias) e cila peshohet, sikurse dhe sinjalet hyrëse. Peshat e hyrjeve dhe animeve mund të konceptohen si koeficientë me vlera që ndryshojnë vazhdimisht gjatë trajnimit të rrjetit. Vlerat paraprake të peshave caktohen zakonisht në mënyrë rastësore brenda intervalit 0 në 0.3. Gjatë çdo cikli të trajnimit, hyrjet e peshuara mblidhen dhe tejçohen tek funksioni i aktivizimit, i njohur ndryshe si funksioni i transferimit. Ky i fundit bën lidhjen midis vlerës shumatore të marë nga hyrja e neuronit me daljen e tij. Emërtimi “funksion i aktivizimit” lidhet me faktin se është pikërisht ky funksion që dikton pragun e aktivizimit të neuronit si dhe forcën e sinjalit në dalje të tij. Rrjetet nervore të sotme përdorin zakonisht funksione jolineare aktivizimi. Kjo i jep mundësi rrjetit që t’i kombinojë hyrjet në mënyra më komplekse, e për pasojë të ketë aftësi më të larta për të modeluar më shumë probleme. Një nga këto funksione aktivizimi është funksioni logjistik i quajtur ndryshe funksioni sigmoidë. Ky funksion ka grafik në formë S-je dhe paraqitet matematikisht nga formula:

Funksioni sigmoidë garanton që dalja e neuronit të jetë gjithnjë midis vlerave 0 dhe 1, pavarësisht nga vlerat e hyrjeve. Një tjetër funksion i rëndësishëm aktivizimi i përdorur masivisht në ditët e sotme eshtë Njësia Lineare e Korrigjuar (ang. Rectified Linear Unit) që shënohet ReLU dhe përllogaritet me anë të formulës:
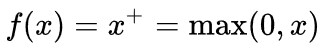
Zgjedhja e funksionit të aktivizimit që përdorim në nyjet e rrjetit varet nga problemi që nga nevojitet të zgjidhim me anë të atij rrjeti. Mund të përdorim p.sh. rrjete me vetëm një nyjë në dalje për të modeluar probleme të regresit linear. Në këtë rast, neuroni i vetëm i daljes mund të përdoret pa ndonjë funksion aktivizimi duke lidhur në mënyrë direkte hyrjet e peshuara me daljen. Rrjete të tjera me një nyjë të vetme në dalje mund të përdoren edhe për probleme të klasifikimit binar. Në këtë rast është e zakonshme që nyja e vetme e daljes të përdori funksionin sigmoidë që jep një vlerë nga 0 në 1 e cila përfaqëson probabilitetin që parashikimi t’i përkasi klasës 1. Në rastet e klasifikimeve shumëklasore përdoren zakonisht rrjete me shumë neurone në dalje, një për secilën klasë. Në këto raste përdore një tjetër funksion aktivizimi i quajtur softmax i cili përllogarit probabilitetin e parashikimit të secilës klasë (për më shumë detaje rreth funksionit softmax kaloni këtu). Klasa e parashikuar konsiderohet ajo probabiliteti i përllogaritur i të cilës është më i larti krahasuar me probabilitetet e klasave të tjera.
Nga ana strukturore çdo rrjet nervor ndjek një topologji të caktuar që varet nga mënyra se si vendosen shtresat e neuroneve kundrejt njëra-tjetrës. Një shtresë nuk është gjë tjetër veçse një rresht neuronesh që aktivizohen në një moment pak a shumë të njëjtë kohe. Të gjithë rrjetet kanë një shtresë neuronesh që quhet shtresa e hyrjes ose shtresa e dukshme. Nëse përhapjen e sinjaleve në rrjet e konceptojmë si një lëvizje nga e majta në të djathtë, atëhere shtresa e hyrjes konsiderohet shtresa që ndodhet në ekstremin e majtë të rrjetit. Neuronet e kësaj shtrese i marrin vlerat nga bashkësia e të dhënave dhe i tejçojnë te shtresa pasuese. Shtresa apo shtresat që vijnë pas shtresës së hyrjes quhen shtresat e fshehura. Rrjetet nervore më të thjeshta (p.sh. rrjeti Perceptron) kanë vetëm një shtresë të tillë me vetëm një neuron apo nyjë e cila gjeneron sinjalin e daljes. Rrjetet që përdoren sot kanë disa shtresa të fshehura dhe quhen rrjete shumështresore. Rrjetet më komplekse kanë shumë shtresa të fshehura të vendosura njëra pas tjetrës dhe për pasojë janë të thella, pra me një largësi të madhe nga hyrja (ekstremi i majtë) te dalja (ekstremi i djathtë). Emërtimi “mësim i thellë” (ang. deep learning) vjen pikërisht nga përdorimi i rrjeteve nervore të thella për zgjidhjen e problemeve të vështira. Në ekstremin e djathtë të rrjetit qëndron shtresa e daljes e cila nxjerr një vlerë dalëse apo një vektor vlerash të tilla në varësi të rastit të përdorimit. Shtresa e daljes konsiderohet ndryshe si shtresa e fundit e fshehur.




